限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: muyang-0410
初中数学中旋转是九年级上册的第三个单元,记二次函数之后旋转的应用以及旋转的性质,在中考当中也占了一定的比例。今天唐老师就给大家详细的讲解,旋转的应用该如何进行学习,以及它都有哪些重要的考点。

一、知识点归纳与总结
1.旋转:将一个图形绕着某点O转动一个角度的变换叫作旋转。其中,O叫做,转动的角度叫作。
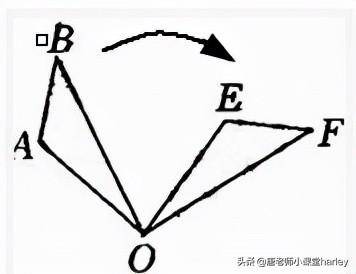
2.旋转性质
⑴ 旋转后的图形与原图形
⑵ 对应线段与O形成的角叫作旋转角
⑶ 各旋转角都相等
3.平移:将一个图形沿着某条直线方向平移一定的距离的变换叫作平移。其中,该直线的方向叫作平移方向,该距离叫作平移距离。
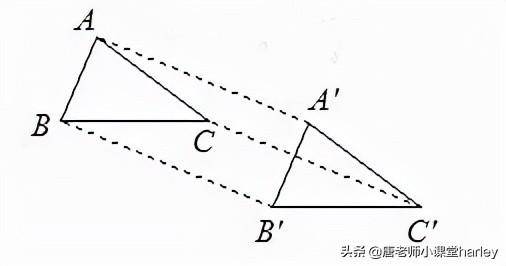
4.平移性质
(1) 平移后的图形与原图形全等
(2) 两个图形的对应边连线的线段(等于平行距离)
(3) 各组对应线段平行且相等
5.中心对称与中心对称图形
(1) 中心对称:若一个图形绕着某个点O旋转180°,能够与另一个图形,则这两个图形关于这个点对称或中心对称。其中,点O叫作对称中心.两个图形的对应点叫作关于中心的对称点。
(2) 中心对称图形:若一个图形绕着某个点O旋转180°,能够与原来的图形完全重合,则这个图形叫作中心对称图形。其中,这个点叫作该图形的。

6.轴对称与轴对称图形
(1)轴对称:若两个图形沿着某条轴对折,能够,则这两个图形关于这条轴对称或它们成轴对称。其中,这条轴叫作对称轴。
注:轴对称的性质:① 两个图形全等;② 对应点连线被对称轴垂直平分
(2)轴对称图形:若一个图形沿着某条轴对折,能够完全重合,则这个图形叫作轴对称图形。
7.点的对称变换
(1)关于原点对称的点的特征
两个点关于原点对称时,它们的坐标的符号相反,即点P(x,y)关于的对称点为P'(-x,-y)
(2)关于x轴对称的点的特征
两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P'(x,-y)
(3)关于y轴对称的点的特征
两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于的对称点为P'(-x,y)
(4)关于直线y=x对称
两个点关于直线y=x对称时,横坐标与纵坐标与之前对换,即:P(x,y)关于直线
y=x的对称点为P'(y,x)
(5)两个点关于直线y=-x对称时,横坐标与纵坐标与之前完全相反,即:P(x,y)关于直线y=x的对称点为P'(-y,-x)
注:y=x的直线是过一三象限的角平分线旋转的性质,y=-x的直线是过二四象限的角平分线。

二、经典例题解析
1.旋转的定义
【例1】下列是中心对称图形的有()
(1)线段;(2)角;(3)等边三角形;(4)正方形;(5)平行四边形;(6)矩形;(7)等腰梯形.
A.2个 B.3个 C.4个 D.5个
【解析】根据中心对称图形的定义:若一个图形绕着某个点O旋转180°,能够与原来的图形完全重合,则这个图形叫作中心对称图形进行判断即可.
练习1. 下列文字中属于中心对称图形的有()
A.干 B.中 C.我 D.甲
练习2. 已知下列图形(1)矩形;(2)菱形;(3)等腰梯形;(4)等腰三角形.其中是轴对称图形,而不是中心对称图形的序号是()
A.(1)(2) B.(2)(3) C.(1)(3) D.(3)(4)
2.轴对称和中心对称
【例2】下列图形中,既是轴对称图形旋转的性质,又是中心对称图形的是()
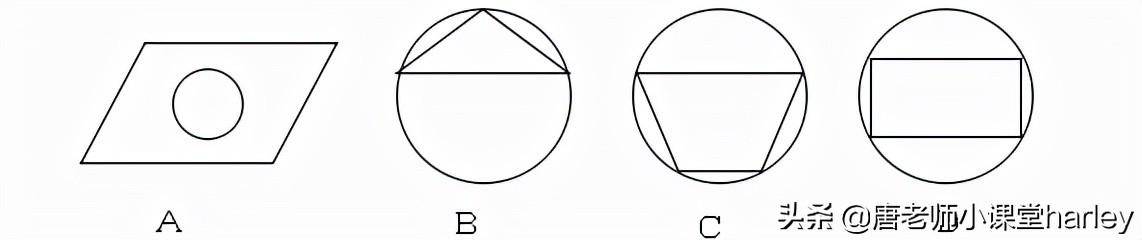
【解析】根据轴对称和中心对称的定义判断即可。

练习3. 下列图形中,既是轴对称图形又是中心对称图形的是()
练习4. 在等边三角形、平行四边形、矩形和圆这四个图形中,即是轴对称图形,又是中心对称图形的有()
A.1个 B.2个 C.3个 D.4个
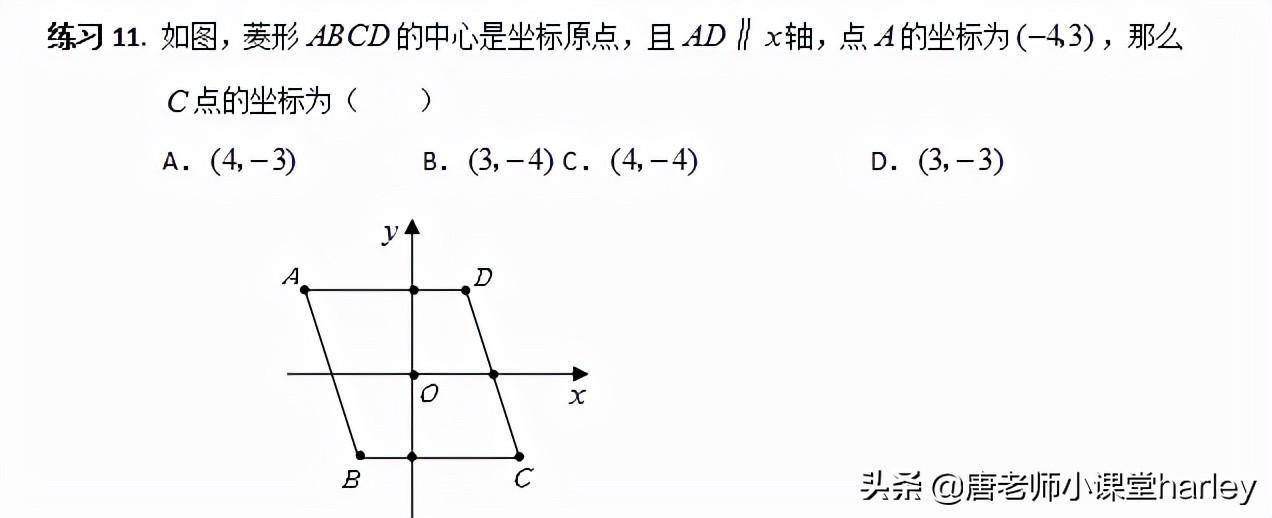
3.坐标的对称
4.对称图形的作法

请输入描述
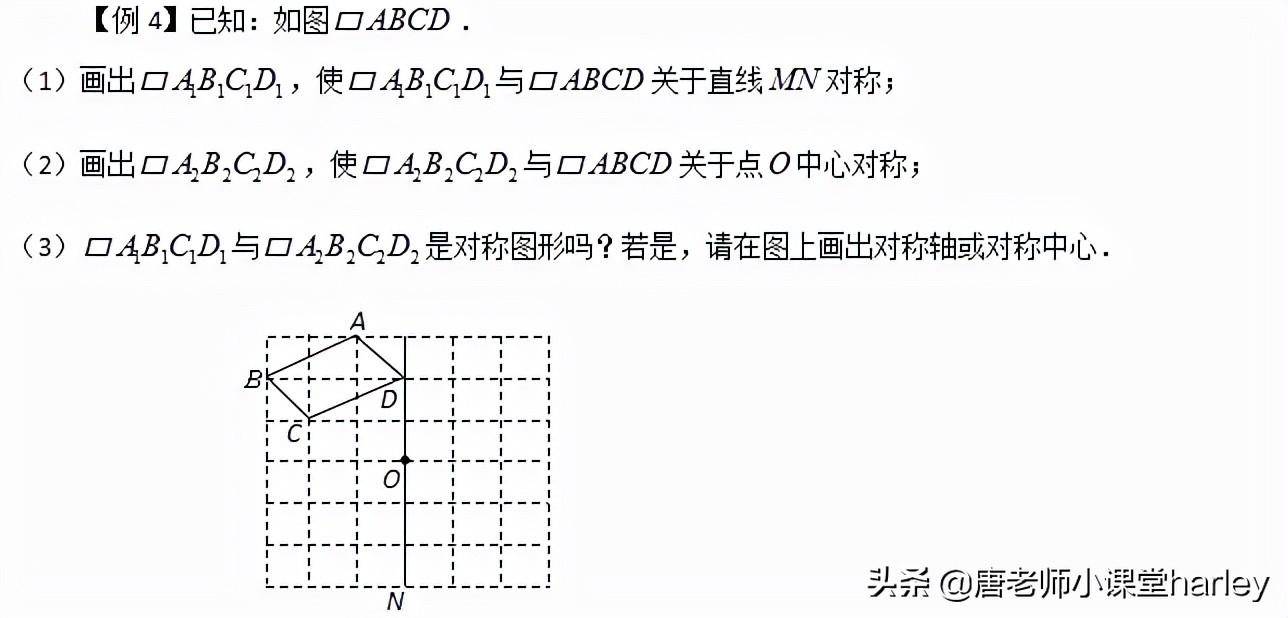
请输入描述
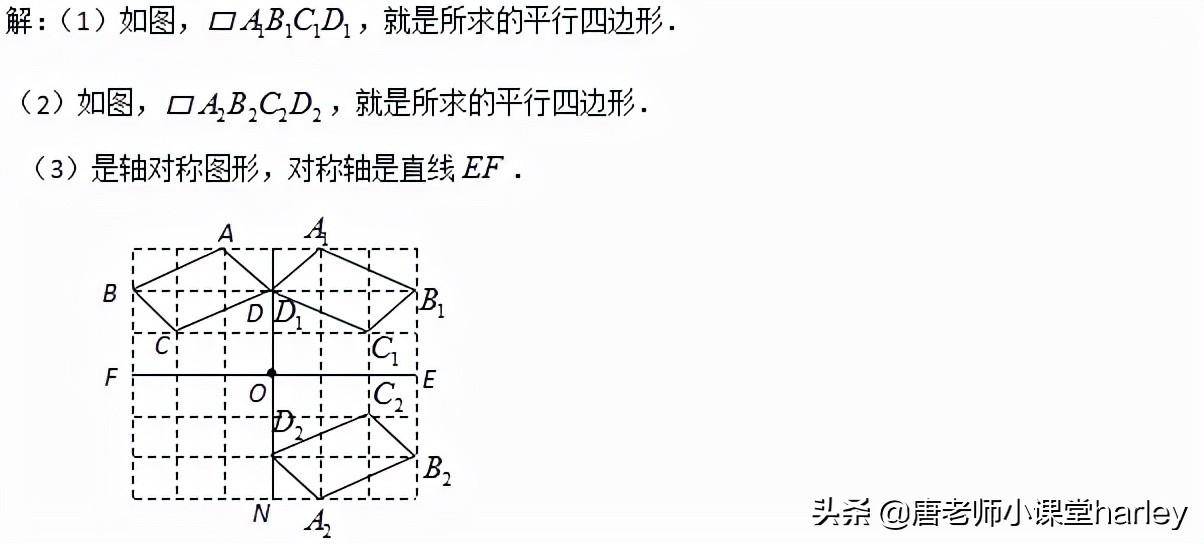
请输入描述

请输入描述
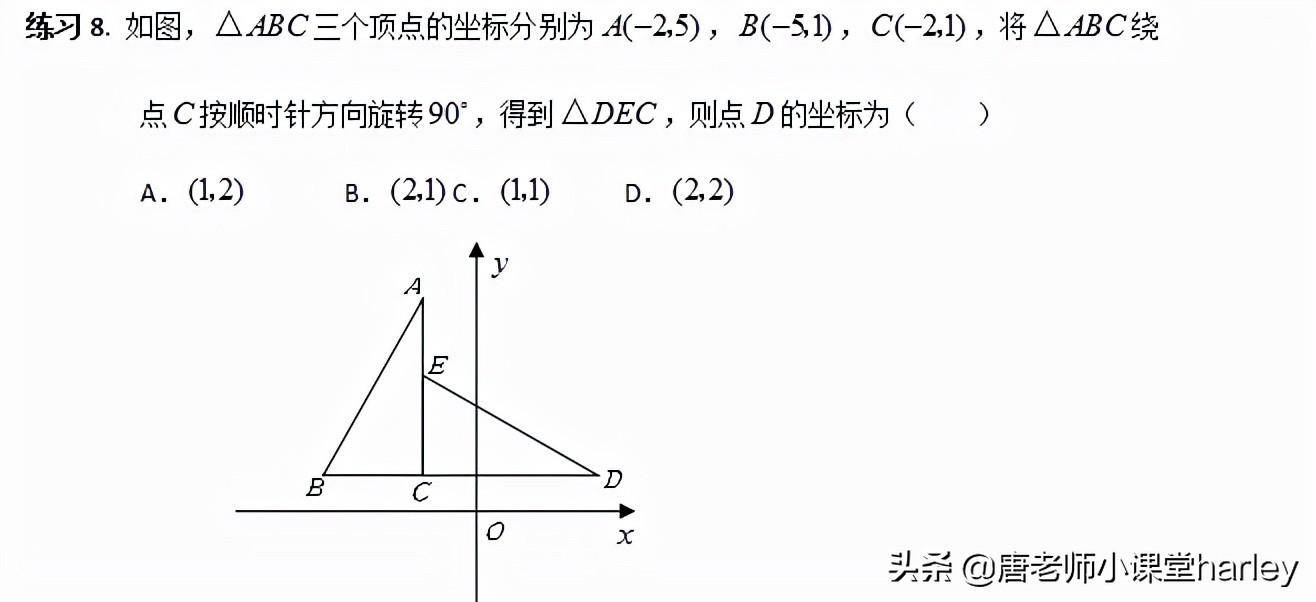
5. 图形的旋转
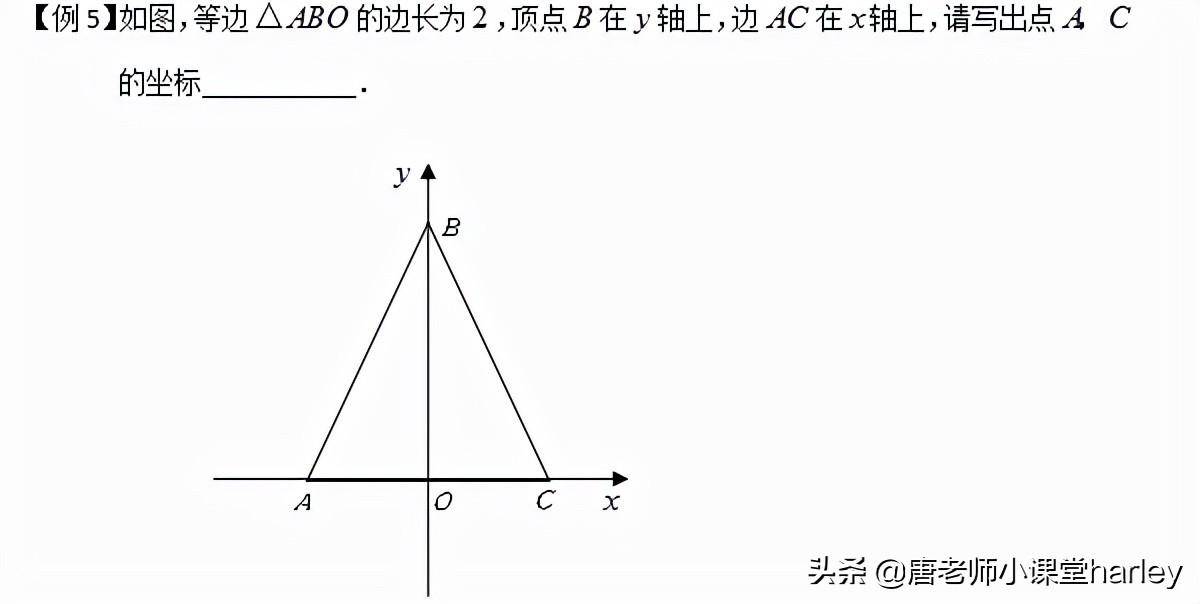
请输入描述
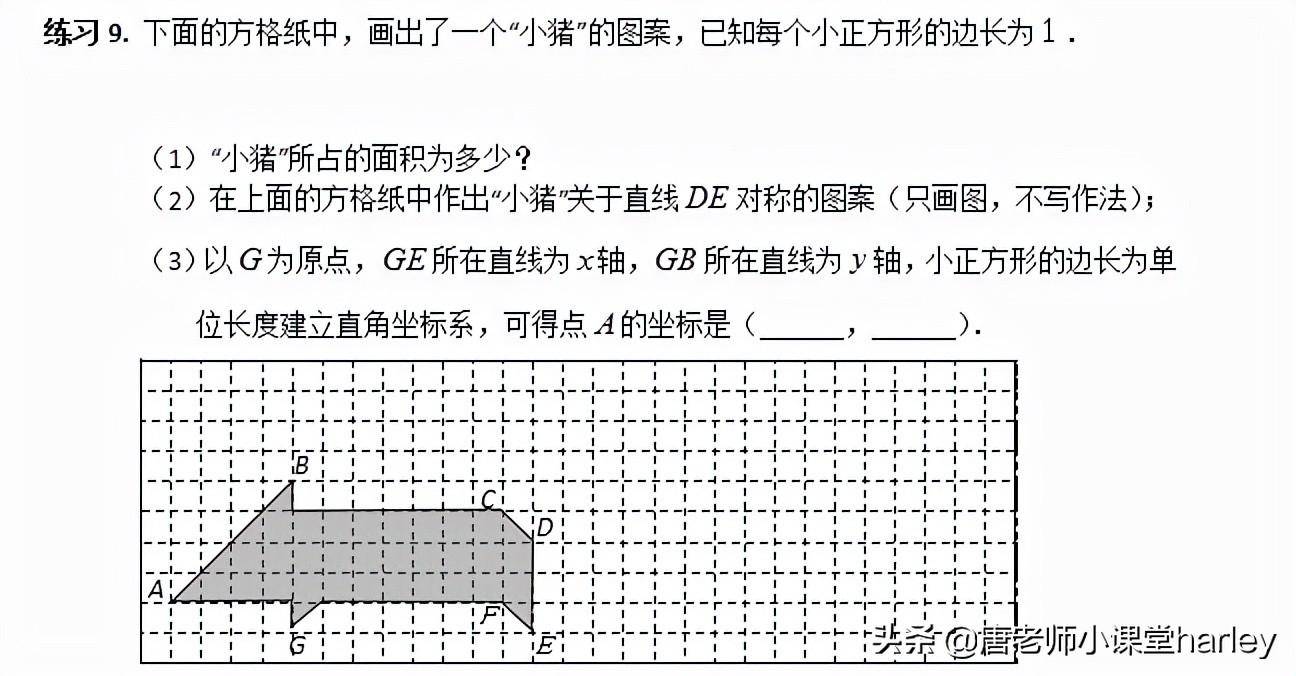
请输入描述

6. 旋转的应用

请输入描述
请输入描述

写在最后:旋转的应用是选利用旋转的定义以及旋转的性质。去解决实际的问题这类题型在平时大家学习看来并不起眼,但是在考试当中其结合其他知识点进行考察是非常普遍的,其中最容易考到的。六大考点已经给大家罗列出来,大家在学习的时候,一定要针对每一个考点进行详细的学习。每个考点最后都配有相应的练习题。
限 时 特 惠: 本站每日持续更新海量各大内部创业教程,一年会员只需98元,全站资源免费下载 点击查看详情
站 长 微 信: muyang-0410






